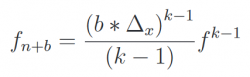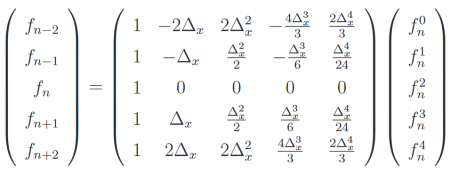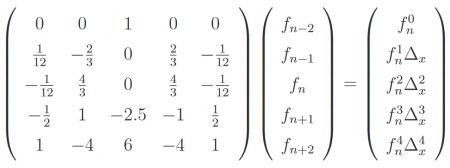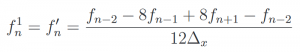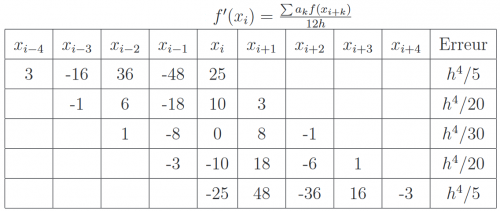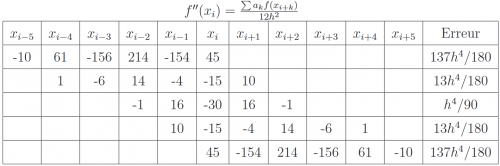Finite difference coefficients

How to calculate coefficients

In this example, I will calculate coefficients for DF4:

Use Taylor series:

So here:

Or in Matrix shape:

Here, we are looking for first derivative, so f_n^1. We only need to invert system to get coefficients. Trick is to move \Delta_x^k on right vector. Resulting matrix is then easy to solve. At the end, we have:

So for our derivative f_n^1:

With the same method, it is possible to get coefficients for all type of derivative, centered and uncentered.

First derivative:

Second derivative:

Coefficients

Central finite difference

This table contains the coefficients of the central differences, for several orders of accuracy.

Derivative	Accuracy	-4	-3	-2	-1	0	1	2	3	4
1	2				-1/2	0	1/2
	4			1/12	-2/3	0	2/3	-1/12
	6		-1/60	3/20	-3/4	0	3/4	-3/20	1/60
	8	1/280	-4/105	1/5	-4/5	0	4/5	-1/5	4/105	-1/280
2	2				1	−2	1
	4			-1/12	4/3	-5/2	4/3	-1/12
	6		1/90	-3/20	3/2	-49/18	3/2	-3/20	1/90
	8	-1/560	8/315	-1/5	8/5	-205/72	8/5	-1/5	8/315	-1/560
3	2			-1/2	1	0	-1	1/2
	4		1/8	-1	13/8	0	-13/8	1	-1/8
	6	-7/240	3/10	-169/120	61/30	0	-61/30	169/120	-3/10	7/240
4	2			1	-4	6	-4	1
	4		-1/6	2	-13/2	28/3	-13/2	2	-1/6
	6	7/240	-2/5	169/60	-122/15	91/8	-122/15	169/60	-2/5	7/240
5	2		-1/2	2	-5/2	0	5/2	-2	1/2

Forward and backward finite difference

This table contains the coefficients of the forward differences, for several order of accuracy.

Derivative	Accuracy	0	1	2	3	4	5	6	7	8
1	1	-1	1
	2	-3/2	2	-1/2
	3	-11/6	3	-3/2	1/3
	4	-25/12	4	-3	4/3	-1/4
	5	-137/60	5	-5	10/3	-5/4	1/5
	6	-49/20	6	-15/2	20/3	-15/4	6/5	-1/6
2	1	1	-2	1
	2	2	-5	4	-1
	3	35/12	-26/3	19/2	-14/3	11/12
	4	15/4	-77/6	107/6	-13	61/12	-5/6
	5	203/45	-87/5	117/4	-254/9	33/2	-27/5	137/180
	6	469/90	-223/10	879/20	-949/18	41	-201/10	1019/180	-7/10
3	1	-1	3	-3	1
	2	-5/2	9	-12	7	-3/2
	3	-17/4	71/4	-59/2	49/2	-41/4	7/4
	4	-49/8	29	-461/8	62	-307/8	13	-15/8
	5	-967/120	638/15	-3929/40	389/3	-2545/24	268/5	-1849/120	29/15
	6	-801/80	349/6	-18353/120	2391/10	-1457/6	4891/30	-561/8	527/30	-469/240
4	1	1	-4	6	-4	1
	2	3	-14	26	-24	11	-2
	3	35/6	-31	137/2	-242/3	107/2	-19	17/6
	4	28/3	-111/2	142	-1219/6	176	-185/2	82/3	-7/2
	5	1069/80	-1316/15	15289/60	-2144/5	10993/24	-4772/15	2803/20	-536/15	967/240

Backward can be obtained by inverting signs.

(source : http://en.wikipedia.org/wiki/Finite_difference_coefficient)

User Tools

Site Tools